Порозрядні операції в JavaScript

Порозрядні операції виконуються над окремими розрядами або бітами чисел. Ці операції виконуються тільки над цілими числами. Але спочатку коротко розглянемо, що являють собою розряди чисел.

Двійкове представлення чисел

На рівні комп'ютера всі дані представлені у вигляді набору бітів. Кожен біт може мати два значення: 1 (є сигнал) і 0 (немає сигналу). І всі дані фактично являють собою набір нулів і одиниць. 8 біт представляють 1 байт. Подібну систему називають двійковою.

Наприклад, число 13 у двійковій системі дорівнюватиме 1101₂. Як ми це отримали:

// переведення десяткового числа 13 у двійкову систему 
13/2 = 6 // залишок 1 (13 - 6 *2 = 1) 
6/2 = 3 // залишок 0 (6 - 3 *2 = 0) 
3/2 = 1 // залишок 1 (3 - 1 *2 = 1) 
1/2 = 0 // залишок 1 (3 - 1 *2 = 1) 
1/2 = 0 // залишок 1 (1 - 0 *2 = 1)

Загальний алгоритм полягає в послідовному діленні числа і результатів ділення на 2 та отриманні залишків, доки не дійдемо до 0. Потім вибудовуємо залишки в лінію у зворотному порядку і в такий спосіб формуємо двійкове представлення числа. Конкретно в цьому випадку по кроках:

Ділимо число 13 на 2. Результат ділення - 6, залишок від ділення - 1 (оскільки 13 - 6 *2 = 1)
Далі ділимо результат попередньої операції ділення - число 6 на 2. Результат ділення - 3, залишок від ділення - 0
Ділимо результат попередньої операції ділення - число 3 на 2. Результат ділення - 1, залишок від ділення - 1
Ділимо результат попередньої операції ділення - число 1 на 2. Результат ділення - 0, залишок від ділення - 1
Останній результат ділення дорівнює 0, тож завершуємо процес і вибудовуємо залишки від операцій ділень, починаючи з останнього - 1101

Під час зворотного переведення з двійкової системи в десяткову множимо значення кожного біта (1 або 0) на число 2 у ступені, що дорівнює номеру біта (нумерація бітів іде від нуля):

// переведення двійкового числа 1101 у десяткову систему 
1(3-й біт)1(2-й біт)0(1-й біт)1(0-й біт) 
1 *²³ + 1 *²² + 0 *²¹ + 1 *²⁰ 
=
1 * 8 + 1 * 4 + 0 * 2 + 1 * 1
=
8 + 4 + 0 + 1
=
13

У JavaScript для визначення чисел у двійковому форматі перед числом застосовується префікс 0b:

const num = 0b1101; // 13 у десятковій системі
console.log(num); // 13

Представлення від'ємних чисел

Для запису чисел зі знаком у JavaScript застосовується додатковий код (two's complement), за якого старший розряд є знаковим. Якщо його значення дорівнює 0, то число позитивне, і його двійкове представлення не відрізняється від представлення беззнакового числа. Наприклад, 0000 0001 у десятковій системі 1.

Якщо старший розряд дорівнює 1, то ми маємо справу з від'ємним числом. Наприклад, 1111 1111 в десятковій системі представляє -1. Відповідно, 1111 0011 представляє -13.
Щоб отримати з додатного числа від'ємне, його потрібно інвертувати і додати одиницю:


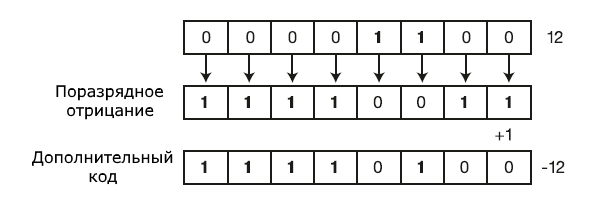Наприклад, отримаємо число -3. Для цього спочатку візьмемо двійкове подання числа 3:

3₁₀ = 0000 ₀₀₁₁₂

Інвертуємо біти

~0000 0011 = 1111 1100

І додамо 1

1111 1100 + 1 = 1111 1101

Таким чином, число 1111 1101 є двійковим представленням числа -3.

Розглянемо, як буде йти додавання числа зі знаком і без знака. Наприклад, складемо 12 і -8:

12₁₀ = 000011002 
+
-8₁₀ = 11111000₂ (8 - 00001000, після інверсії - 11110111, після +1 = 11111000) 
=
4₁₀ =00000100₂

Ми бачимо, що в двійковій системі вийшло число 00000100₂ або 4₁₀ у десятковій системі.

Ми можемо це побачити на практиці:

let num = 0b1100; // 12 у десятковій системі
num = ~num; // інверсія розрядів
num = num + 1;
console.log(num); // -12

Операції зсуву

Кожне ціле число в пам'яті представлено у вигляді певної кількості розрядів. І операції зсуву дають змогу зсунути бітове представлення числа на кілька розрядів вправо або вліво. Операції зсуву застосовуються тільки до цілочисельних операндів. Є дві операції:

<< (зсув уліво)

Зсуває бітове представлення числа, представленого першим операндом, уліво на певну кількість розрядів, яку задає другий операнд.

const res = 2 << 2; // 10 на два розряди вліво = 1000 - 8
console.log(res); // 8

Число 2 у двійковому поданні 0010₂. Якщо зрушити число 0010 на два розряди вліво, то вийде 1000, що в десятковій системі дорівнює числу 8.

>> (арифметичне зрушення вправо)

Зсуває бітове подання числа вправо на певну кількість розрядів.

const res = 16 >> 3; // 10000 на три розряди вправо = 10 або 2 у десятковій системі
console.log(res); // 2

Число 16 у двійковому поданні 10000₂. Якщо зсунути число 10000 на три розряди праворуч (три останні розряди відкидаються), то вийде 00010, що в десятковій системі являє собою число 2.

Варто зазначити, що це так званий арифметичний зсув, під час якого зсунуті в лівій частині розряди заповнюються знаковим бітом - 0 для додатних і 1 для від'ємних чисел. Таким чином, при зсуві від'ємних чисел не буде побоювання, що після зсуву вони стануть додатними. Наприклад:

const res = -16 >> 3; // 11111110000 на три разряда вправо = 1111111111111110
console.log(res); // -2

Так, при зсуві вправо -16 на 3 розряди ми отримаємо -2, що цілком природно.

>>> (логічне зрушення вправо)

Зсуває бітове подання числа вправо на певну кількість розрядів, але на відміну від операції >> заповнює зсунуті в лівій частині розряди нулями, тобто ми отримуємо беззнакове зсув. Таким чином, навіть якщо ми зсуваємо від'ємне число, на виході ми в будь-якому разі отримаємо позитивне:

const res = -16 >>> 3;
console.log(res); // 536870910

Можна помітити, що зсув на один розряд ліворуч фактично аналогічний множенню на 2, тоді як зсув праворуч на один раз еквівалентний діленню на два. Ми можемо узагальнити: зсув ліворуч на n аналогічний множенню числа на ²ⁿ, а зсув праворуч на n розрядів аналогічний діленню на ²ⁿ, що можна використовувати замість множення/поділу на ступені двійки:

const res1 = 8 << 2; // еквівалентно 8 * 4
console.log(res1); // 32

const res2 = 64 >> 4; // еквівалентно 64 / 16
console.log(res2); // 4

Порозрядні операції

Порозрядні операції також проводяться тільки над відповідними розрядами чисел:

&: порозрядна кон'юнкція (операція І або порозрядне множення). Повертає 1, якщо обидва з відповідних розрядів обох чисел дорівнюють 1
|: порозрядна диз'юнкція (операція АБО або порозрядне додавання). Повертає 1, якщо хоча б один із відповідних розрядів обох чисел дорівнює 1
^: порозрядне виключне АБО. Повертає 1, якщо тільки один із відповідних розрядів обох чисел дорівнює 1
~: порозрядне заперечення або інверсія. Інвертує всі розряди операнда. Якщо розряд дорівнює 1, то він стає рівним 0, а якщо він дорівнює 0, то він отримує значення 1.

Застосування операцій:

const a = 5 | 2; // 101 | 010 = 111 - 7
const b = 6 & 2; // 110 & 010 = 10 - 2
const c = 5 ^ 2; // 101 ^ 010 = 111 - 7
const d = ~9; // -10

Наприклад, вираз 5 | 2 дорівнює 7. Число 5 у двійковому записі дорівнює 101, а число 2 - 10 або 010. Додамо відповідні розряди обох чисел. Під час додавання якщо хоча б один розряд дорівнює 1, то сума обох розрядів дорівнює 1. Тому отримуємо:

1 0 1
0 1 0
1 1 1

У підсумку отримуємо число 111, що в десятковому записі представляє число 7.

Візьмемо інший вираз 6 & 2. Число 6 у двійковому записі дорівнює 110, а число 2 - 10 або 010. Помножимо відповідні розряди обох чисел. Добуток обох розрядів дорівнює 1, якщо обидва ці розряди дорівнюють 1. Інакше добуток дорівнює 0. Тому отримуємо:

1 1 0
0 1 0
0 1 0

Отримуємо число 010, що в десятковій системі дорівнює 2.

Посібник по JavaScript